結び目 の 数理
ライザ の アトリエ 草刈り 鎌研究集会「結び目の数理VI」. 最終更新日: 12/12/2023 04:01:29. 研究集会「結び目の数理 IV - Waseda University. 研究集会「結び目の数理 IV 」 トポロジー連絡会議の支援するトポロジープロジェクトの一環として、 2021年度科学研究費補助金 基盤研究(A)「3次元双曲多様体上の量 …. 現場 を 空ける
なんでも ご たれ 取扱 店研究集会「結び目の数理III」報告集. 交点数が3以下の long virtual knot について 井町 翔太朗 (京都大学数理解析研究所) 結び目外部空間のスケイン加群に関連する pairing の計算について 田内 光一 (筑波大学理工 …. 結び目の数学 ~身近な対象から未解明の科学的命題まで . 具体的には、同じ結び目なら同じ値を取る量(結び目不変量)を用いますが、結び目不変量の構成に幾何、代数、解析、統計などの数学が用いられます。 日本は結び目理 …. 研究集会「結び目の数理Ⅴ」 - プログラム・アブストラクト. 結び目 (K)、結び目群 (G(K)) に対し、Ma-Qiu 指数とは、(G(K)) の交換子部分群を正規に生成する元の最小数のことで、中西指数とは、(K) の結び目加群の生成元の最 …. 研究集会「結び目の数理 IV 」報告集 - Waseda University. 研究集会「結び目の数理 IV 」報告集. 研究集会「結び目の数理 IV 」報告集. (1) 一括版(18.4MB) (2)分割版 門上 晃久(金沢大学大学院自然科学研究科) Continued …. 研究集会「結び目の数理VI」. 研究集会「結び目の数理VI」. トポロジー連絡会議の支援するトポロジープロジェクトの一環として,. 科学研究費補助金 (基盤研究 (A))「3次元双曲多様体上の量子トポロ …. 研究集会「結び目の数理 IV 講演アブストラクト集 - Waseda . のペアリングはコホモロジーのカップ積で記述できる為、その符号数の計算が比較的可能である。実際、スライスではない結び目の新しい例を与えた。大倉拓実氏(東京工 …. 研究集会「結び目の数理Ⅴ」 - Google Sites. 研究集会「結び目の数理Ⅴ」 日本数学会トポロジー分科会トポロジー連絡会議・トポロジープロジェクトの一環として,標記の研究集会を以下の日程で開催いたしました …. 結び目理論 - Wikipedia. 結び目理論 ( むすびめりろん、knot theory )とは、紐の 結び目 を数学的に表現し研究する学問で、 低次元位相幾何学 の1種である。 組合せ的位相幾何学 や 代数的位相 …. 研究集会「結び目の数理III」. 研究集会「結び目の数理III」 トポロジー連絡会議の支援するトポロジープロジェクトの一環として, 科学研究費補助金(基盤研究(A))「結び目と3次元多様体の量子トポロ …. 結び目の数学 京都大学数理解析研究所 鈴木咲衣 - 東京工業大学. 結び目の数学京都大学数理解析研究所. 鈴木咲衣. 川崎 姫 の 回春
5 ステップ トリートメント と は2012 年8 月1日@愛知県立明和高校. 目次. 1.結び目って? 2.結び目の不変量を計算してみよう3.私の研究のお話4.まとめ. 1. …. 結び目の数学 京都大学数理解析研究所 鈴木咲衣 - 東京工業大学. 結び目の数学京都大学数理解析研究所. 鈴木咲衣. 2016 年3 月4日@兵庫県立龍野高校. 目次. 1.結び目って? 2.結び目で数学してみる3.結び目の不変量を計算してみよう4.私の …. 結び目の数学 白眉センター・数理解析研究所 鈴木咲衣. 結び目. 関係性を理解したい。 ( 例) 自然数 N= { 1, 2, 3 , , , } かけ算:2×3 = 6, 4×7=28, , 6 1 7. 3 2. 2 つの自然数 a, b に対して, もうひとつの自然数a×bを対応させる操作. (2, 3)→ …. 結び目の数学. 1 序. 結び目理論は、現在とても活発に研究されている分野で、それ自体の面白さはもちろんのこと、数学内外の最先端の研究分野との結びつきも、とても興味深いもので …. 結び目の数学 - Research Institute for Mathematical Sciences. 1.1 結び目の和. 中空 ポリカ 建具
土地 購入 不動産 屋 に 聞く こと結び目の集合で,イソトピックな結び目を同一視した集合を. = { 結び目}/ ∼とおく.結び目の二項演算. × K → K. を以下のように定義し,結び目の連結和と呼ぶ. …. 研究集会「結び目の数理」報告集 - Waseda University. 研究集会「結び目の数理」報告集. 上 五島 の 防波堤 釣り
彼氏 を いかせる(1) 一括版(16MB) (2) 分割版 瀧村祐介(学習院中等科) Crosscap number and knot projections (伊藤昇氏(東大数理)との共同 …. 結び目 (数学) - Wikipedia. 厳密な定義. 結び目 とは、 円周 あるいは 一次元球面 S1 の 三次元空間 R3 への 埋め込み を言う [1] 。 文献によっては コンパクト空間 である 三次元球面 S3 への埋め込みを …. Yoshiyuki Ohyamas home page - TWCU. 東京女子大学現代教養学部教授. 専門:位相幾何学,特に結び目理論. 研究テーマ. 1.結び目の局所変形. 2.結び目の Vassiliev 不変量の研究. 3.仮想結び目の研究. 4.空 …. 中村 伊南沙 – 佐賀大学. MESSAGE 曲面結び目は、その構成法もあまり知られていないのが現状です。不変量についても、すべての図式を考えたときに、各図式に現れる3重点の数の最小値である …. 「この紐、ほどける?」-結び目理論への誘い- | 数学・統計教室 . 結び目理論を使った結び目の判定方法として「多項式」や「数値」を使った古典的な方法があります。 つまり、結び目の絡まり具合の情報から多項式や …. 数学者を目指す|さのたけと - note(ノート). 数学者を目指す. 6. さのたけと. 2024年3月13日 20:59. (本記事は 『数学セミナー』2023年4月号 に寄稿した記事を、編集者の方の許可を頂いて転載したもので …. 研究集会「結び目の数理」 - Waseda University. き ばい やん せ 焼酎
カビ を 吸い込ん だ 処置1998年度から10回開催された研究集会「結び目のトポロジー」シリーズを継承して、 2018年度より新シリーズとなる研究集会「結び目の数理」を開催いたします。. 例 …. 数理・計算科学系. 数理・計算科学系:研究内容. 5. 私の研究室では、非線形偏微分方程式の数学的な解析を行っています。. 特に、流体、プ ラズマ、半導体中の電子の挙動など物理現象を記 …. 三つ編みツインテールに韓国風ハーフアップ♡卒園式、入学式 . 保育園や幼稚園の卒園式、小学校の入学式、親戚の結婚式のお呼ばれなど、特別な日の子ども、中でも女の子… お姉さん世代で話題沸騰中! 韓国アイドルっぽいツ …. 結び目からTバックだけを纏った下半身が露わに…ケイティ . 結び目からTバックだけを纏った下半身が露わに…ケイティ・ペリー、セクシーすぎるドレスが話題に! 【関連記事】 【写真】結び目からのぞく . 研究集会「結び目の数理」 講演アブストラクト集 - Waseda . 本講演は瀧村祐介氏(学習院中等科)との共同研究である。結び目のクロスキャップは1978年 にClark氏により導入され、その論文で結び目がクロスキャップ1であること …. エルサ風、ハート三つ編み…卒園式、入学式の簡単ヘア . ①顔周りの髪を残しておき、耳の付け根のラインで平行に髪を取って、後ろでハーフアップにします。 【STEP1】くるりんぱを作り、少し毛を引き出す ②結び目の …. ボッテガ・ヴェネタ“結び目フック”のバッグ「アンディアー . ボッテガ・ヴェネタ“結び目フック”のバッグ「アンディアーモ」カーフスキン×キャンバスに. ボッテガ・ヴェネタ (BOTTEGA VENETA)の2024年夏コレクションから …. 研究集会「結び目の数学 V - Waseda University. 篠島 離宮 真砂 悠々庵
約束 の ネバーランド 鬼 の 頂点研究集会「結び目の数学 V 」. 地図はこちら プ ログラム( pdf 版) ア ブストラクト集( pdf 版) 研 究集会報告集 球面上の結び目射影図の領域の不可避集合について On the …. 研究集会「結び目の数理VI」講演アブストラクト. 研究集会「結び目の数理VI」講演アブストラクト 12月23日(土) 佐藤衡(埼玉大学大学院理工学研究科) 多面体空間グラフによる多面体のn 重covering 多面体空間グラフP が多面体P ′をn 重covering するとは、多面体P の covering としてP′ の近傍に構成される多面体空間グラフP からのある種の被覆. Information on the Morse-Novikov number. ファイバー結び目の体積表示, (森藤孝之氏との共同研究) 研究集会「結び目の数理V」 日本大学文理学部 2022年12月24日. ファイバー結び目の体積表示, (森藤孝之氏との共同研究) 山梨大学トポロジーセミナー 2022年3 …. 題目: 結び目の数理と物理 - 東京大学. 題目: 結び目の数理と物理. 日時: 2012年9月7日 (金)9:30~9日 (日)17:40 *終了しました. 会場: 東京大学大学院数理科学研究科大講義室. 京王井の頭線 駒場東大前駅下車. 駒場キャンパスへの来方 駒場キャンパス地図. 講師・講演題目. 出口哲生 (お茶の水女子大物理 . 結び目の数学Ⅱアブストラクト付きプログラム - Waseda University. 10:40-11:10 後藤 彩(奈良女子大学大学院人間文化研究科) 2元生成メビウス変換群におけるBowditchの条件について アブストラクト:2橋結び目の双曲構造を調べる上で2元生成メビウス変換群の研究は非常に重要である。. BowditchおよびTanらはこれらに対しQ条件と . 守 破 離 の 精神
松 ヤニ を 落とす 洗剤研究集会「結び目の数理VI」. 最終更新日: 12/12/2023 04:01:29. 検索詳細 |日本大学 研究者情報システム. 研究集会「結び目の数理 V 企画立案・運営等 市原 一裕,松土恵理,茂手木公彦 (日本大学文理学部), 日本大学文理学部 百周年記念館 国際会議場, 2022年12月21日 - 2022年12月23日 研究集会『トポロジーとコンピュータ …. Yoshiyuki Ohyamas home page - TWCU. 研究集会「結び目の数理 III」(2020年12月23日から26日まで) 著書,解説記事 1. 共訳 「結び目の数学と物理」, 鈴木晋一,河内明夫監訳, 培風館, 平成7年10月. 2.現代数学スナップショット「量子不変量をめぐって」第3 回 . 数学入門公開講座 バックナンバー(講義ノート)|京都大学 . この講義では、結び目の数学を基礎からゆっくりお話し、結び目の不変量であるジョーンズ多項式を計算します。 . 
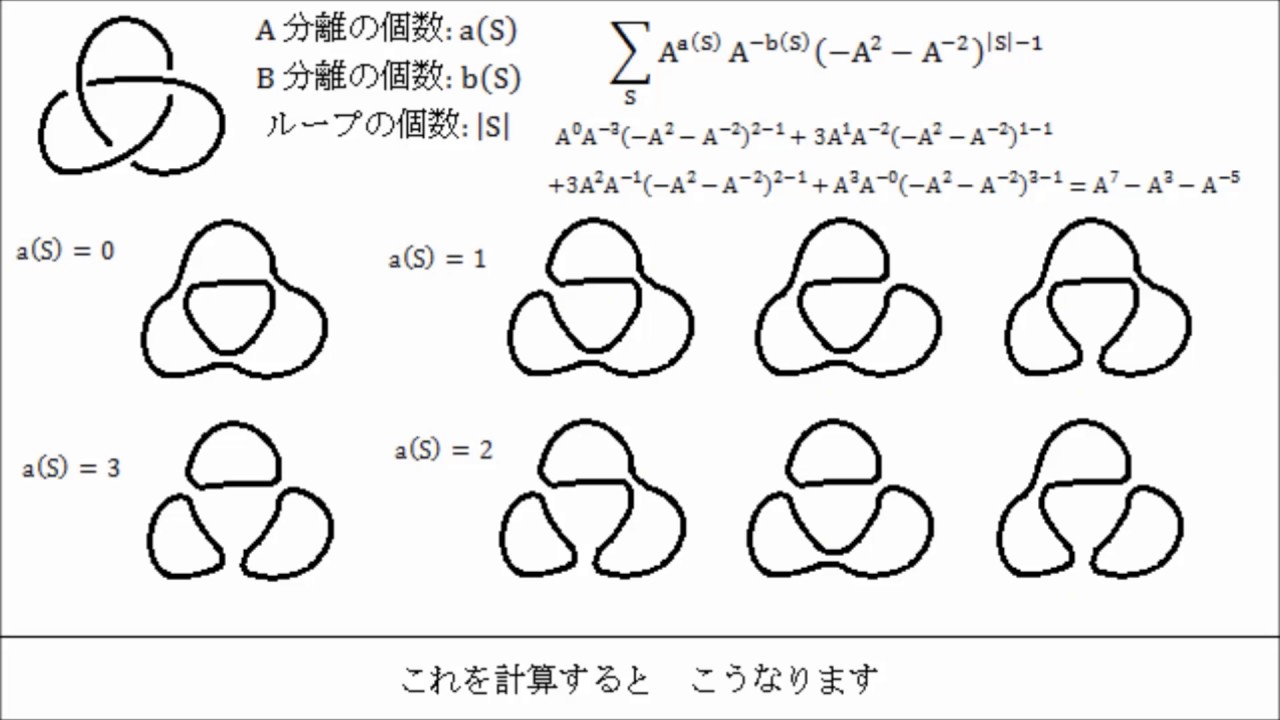
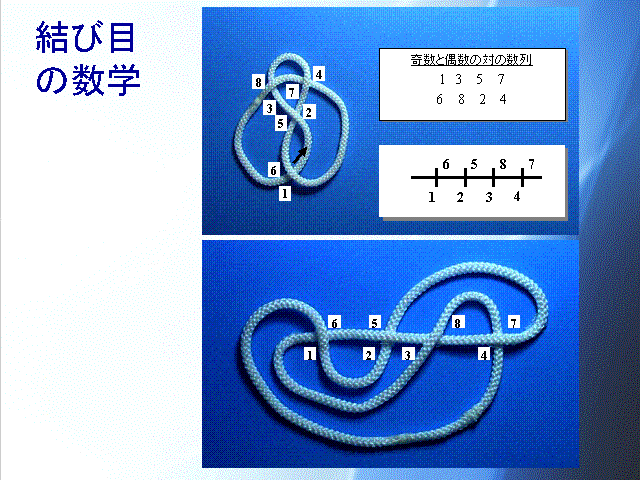
げんき の 杜ひもを結ぶと、結び目ができる。結び目に対して定められる値で、結び目を変形することに関して不変であるようなものを不変量という。不変量を用いて、様々な結び目のタイプを区別することができる。 1980年代を境に、数理物理的手法がトポロジーに導入されて、3次元トポロジーにおいては . 石川 勝巳(数理解析研究所 基礎数理研究部門) | 京都大学 教育 . 結び目や3次元多様体など、低次元トポロジーの対象について、種々の不変量を用いた研究や、それら不変量そのものについての研究を行っている。特にカンドルと呼ばれる代数系を用いた不変量について研究を行ってきたが、これからはこうした理論を拡張することで古典的な群の理論に . 米澤 康好 (Yasuyoshi Yonezawa) - マイポータル - researchmap. 京都大学 数理解析研究所 平成27年度共同利用研究計画 (RIMS合宿型セミナー) 2015年8月. 米澤 康好. researchmapは、日本の研究者情報を収集・公開するとともに、研究者等による情報発信の場や研究者等の間の情報交換の場を提供することを目的として、国立研究 . 新國 亮のウェブサイト - TWCU. Japanese/ English / Twitter 新國 亮のウェブサイトです.. 研究集会「結び目理論」 を開催しました (2月14日, 東京女子大学). 講演もしました. 関係の皆様に深く感謝申し上げます. 研究集会「結び目の数理Ⅵ」 を開催しました (12月23〜26日, 東京女子大学). 関係の皆 . 谷山公規. 谷山 公規(たにやま こうき)のウェブページ [English Page] / / / /. 星型図形(画像をクリックすると拡大画像が別窓で開かれます。. ). 研究集会「結び目の数理 VI 」講演「Pairs of knot invariants」スライド(2023年12月25日). 谷山公規公式プロフィール . 結び目の数学 - 丸善出版 理工・医学・人文社会科学の専門書 . 
村民 の 森 あいの 沢 キャンプ 場上の定理は非可換で無限位数の群が作用するコルクの最初の例と なっており、これは[Tan16, Question 1.5] に答える。増田宙斗 (慶應大学) 非可換群が作用する同変コルクについて 結び目の数理 6 / 18. 組みひもの数理[新装版]|日本評論社. 組みひもの数理[新装版]。河野俊丈氏。日本評論社は1918年創業。法律時報、法学セミナー、数学セミナー、経済セミナー、こころの科学、そだちの科学、統合失調症のひろば、など評価の高い雑誌を定期刊行しています。. Knot Theory on WWW - 広島大学. 別冊「数理科学」(特集:多様体の広がり),サイエンス社,2008年4月号 臨時別冊「数理科学」(特集:3次元トポロジーの新展開),戸田正人(著),サイエンス 社,2007年7月号 「数学の楽しみ」(フォーラム:結び目の不思議). 結び目理論とその応用|日本評論社. 結び目理論とその応用。村杉邦男氏。日本評論社は1918年創業。法律時報、法学セミナー、数学セミナー、経済セミナー、こころの科学、そだちの科学、統合失調症のひろば、など評価の高い雑誌を定期刊行しています。. 研究集会「結び目の数理III」. 科学研究費補助金(基盤研究(A))「結び目と3次元多様体の量子トポロジー」 (研究代表者:大槻 知忠,課題番号:16H02145) の支援を受け,下記の日程で研究集会「結び目の数理III」を開催しました.関係の皆様に感謝申し上げま …. 中西 康剛 - Kobe University. 中西 康剛. 神戸大学理学部数学科. 構造数理講座 教授. 結び目理論教育研究分野. ホームページ. E-mail: Tel: 078-803-5615. 研究テーマ:. 局所的変形による結び目の研究. 結び目は、文化人類学の対象になるほどに古くから、 また、身近なものとして扱われてき . 平澤 美可三のホームページ - NITech. Index. 平澤 美可三のホームページ. 名前:平澤 美可三 (Mikami HIRASAWA) 専門:数学. 研究テーマ: 結び目理論を中心とした三次元多様体のトポロジーの研究. 所属: 名古屋工業大学 大学院 工学研究科 情報工学専攻 情報数理分野 (略称 名工大 数学教室) 所在地 . 結び目理論入門レジュメ - kitasato-u.ac.jp. [結び目理論の主問題(未解決)] 同値でない結び目(絡み目)をすべてリストアップせよ. 定義6 [射影図] 結び目を平面状に射影したもの(例3の図)をその結び目の射影図(diagram) という. a350 ー 1000 カタール 座席
有限長の線分のあつまりとして結び目を表し, ひもの上下は交点 で表す. 講演者募集. 講演を希望される方は,2023年11月12日(日)までに以下のリンク先のフォームから講演申込を行なって下さい. 研究集会「結び目の数理VI」講演申込フォーム 講演時間は質疑応答を合わせて30分を予定しています(申込者多数の場合,短縮の可能性があります).. 研究集会「結び目の数理VI」. の支援を受け,下記の日程で研究集会「結び目の数理VI」を開催しました.関係の皆様に感謝申し上げます. 日時: 2023年12月23日(土) 〜 12月26日(火) 会場: 東京女子大学24号館(安井てつ記念ホール)24202教室 (地図) 新 …. おみくじの数理 - xsrv.jp. おみくじの数理 おみくじの数理というと、「大吉」や「中吉」、「小吉」、「末吉」はたまた「大凶」などの出現 . 次のように折って、結び目を作る。 このとき、結び目がちょうど「正5角形」になっている というわけである。 …. 組みひもの数理[新装版] | 河野 俊丈 |本 | 通販 | Amazon - アマゾン. 組みひもを数理的に取り扱う方法を、豊富な図を用いてやさしく解説する。新たに付録として、「組みひもと圏論」を加筆した。【目次】 第1話 アルティンの組みひも群 運動する点と組みひも 組みひもの構成要素 組みひも関係式 組みひも群の積構造 組みひもとアミダくじ 第2話 リ …. 研究集会「結び目の数理III」講演アブストラクト. 研究集会「結び目の数理III」講演アブストラクト 12月23日(水) 村尾智(早稲田大学) ハンドル体結び目のMCQ ねじれAlexander 不変量 (石井敦氏(筑波大学) との共同研究) 多重共役カンドル(MCQ)とは,ハンドル体結び目図式のReidemeister. Knotting Nagoya 2018 - NITech. 結び目の数理セミナー Knotting Nagoya 会合案内 メインへ 2019年2月会合 「学生合同発表会」 日時:2月17日(日)14時 ~ 場所 : 名古屋工業大学 53号館 3階 5238 教室 466-8555 名古屋市 昭和区 御器所町 名古屋工業大学 .